0.1+0.2不等于0.3?浅谈软测中精度问题是怎么产生的

假设一个用户他银行卡里有资金￥1010.3
购物的时候购物车两个商品分别为￥1000.1，￥10.2，一起结算时，因为没做处理导致系统在支付时计算1000.1+10.2=1010.3000000000001>1010.3导致无法支付成功，提示余额不足，这样的问题显然是非常糟心的。

因为做的项目多，JS、JAVA、PHP、GO、Python语言的精度问题一个不小心都遇了个遍，我把精度问题简单分为两类
1、二级制计算机弊端导致的浮点数计算误差
2、不同语言对浮点数的舍弃不都是四舍五入

二进制计算机弊端

由于我们的世界通用的是十进制，而计算机实际存储、计算时，使用的都是二进制且有长度限制，问题在于十进制数有很多无法转为有限位的二进制数，而计算机的存储容量是有限的，那么实际存储和运算的时候就会拿不精确的二进制数，这就导致了第一步的精度丢失。
为此会遇到两个精度问题
1、如果数值过大，超过类型的限制，则会出现精度丢失，比如js处理9007199254740993会处理为9007199254740992（注：Python无此问题，因Python的整数没有存储位上限）

2、如果数值存在小数点（即浮点数），则会遇到类似十进制1/3这种无法用有限位表示的情况，比如0.1，在处理时只能表示为一个接近0.1的二进制数
十进制0.1的二进制，1001循环，根本无法写完：

0.0001100110011001100110011001100110011001100110011001......

十进制0.2的二进制，1100循环，也是写不完：

0.0011001100110011001100110011001100110011001100110011......

两个精度有丢失的数，进行运算，就可能出现偏离大的情况
比如0.1+0.3计算是不等于0.3，而是0.30000000000000004的情况
但是能精确表示为有效位的十进制0.5和精度有丢失的0.1、0.2、0.3、0.4、0.6、0.7、0.8、0.9进行运算，则运算结果不会离谱的精度丢失（原因是该精度丢失在计算机的把控之内，就算近似处理后还可以还原准确的十进制）

技术解决方案

针对不同领域，有不同精度的解决方案。

如果是要求完全精确的运算，比如要求(1/3)*(6/5)得到的结果为2/5而不是0.3999999...，那么就需要借助fractions方案（主流语言也都有提供）。这个库实现了以分数输入，以分数存储，以分数运算（简化的原理就是所有数转为相同分母，并且分子转为整数进行运算），为此无论前后经过多少次运算，结果都是精确无误差。

对于电商、金融，最多最常见的就是dicimal，能进行高精度的运算。dicimal顾名思义是专门处理十进制的模块，大致原理就是把小数乘以10的整数倍，使得运算变成整数运算，从而避免精度问题（但是如果误用还是会导致精度丢失，如下面例子所示）。

多种语言都使用了decimal（有些语言也叫Bigdecimal）来专门解决精度问题，

例如Python中正确处理0.1+0.2的运算：

from decimal import Decimal
# Decimal传递的为字符串类型的数值
print(Decimal('0.1')+Decimal('0.2'))
# 输出：Decimal('0.3')

Java中正确处理0.1+0.2的运算：

# BigDecimal传递的为字符串类型的数值
BigDecimal a = new BigDecimal("1.01");
BigDecimal b = new BigDecimal("1.02");
System.out.println(a.add(b));

注意，用Decimal不是万事大吉，有使用陷阱，传递的是浮点数，一样会丢失精度
假如上面的Python代码改为：

from decimal import Decimal
# 给Decimal传递浮点数
print(Decimal(0.1)+Decimal(0.2))
# 输出：0.3000000000000000166533453694

假如上面的Java代码改为：

# BigDecimal传递浮点数
BigDecimal a = new BigDecimal(1.01);
BigDecimal b = new BigDecimal(1.02);
System.out.println(a.add(b));
# 输出:2.0300000000000000266453525910037569701671600341796875

对于使用Decimal，Python、Java的Decimal代码注释说明Decimal()传参为浮点数还是会丢失的问题：

Note that Decimal.from_float(0.1) is not the same as Decimal('0.1').
Since 0.1 is not exactly representable in binary floating point, the
value is stored as the nearest representable value which is
0x1.999999999999ap-4. The exact equivalent of the value in decimal
is 0.1000000000000000055511151231257827021181583404541015625.
译：
注意Decimal.from_float(0.1) 与 Decimal('0.1') 不同。由于 0.1 在二进制浮点中不能精确表示，因此该值存储为最接近> 的可表示值，即 0x1.999999999999ap-4。十进制值的精确等值是
0.1000000000000000055511151231257827021181583404541015625。

不同语言舍弃算法

不同语言中的近似值算法，都不一样，我们从小学的就是四舍五入是半向上算法，1.45保留一位小数结果就是1.5，但是如果使用银行家舍弃算法，那结果就是1.4，而实际上还有其他的舍弃算法（舍入到最接近的倍数、舍入到最接近的0.5的倍数、舍入到最接近的负无穷大等）

我先总结：

JavaScript:
使用 Math.round() 进行四舍五入，遵循半向上规则。
对于特定的舍入策略，如银行家舍入，可以使用 toFixed()（虽然返回字符串）或自定义逻辑。

Python:
使用 round() 函数，默认采用半向上规则。
对于金融应用，推荐使用 decimal 模块的 quantize() 方法实现银行家舍入。

Java:
Math.round() 用于基础四舍五入，但其行为在整数和浮点数上有所不同。
BigDecimal 类提供了更精确的控制，包括银行家舍入(ROUND_HALF_EVEN)。

C/C++:
基础的 (int)x 或 (int)(x + 0.5) 实现简单四舍五入，但不适用于所有情况。
使用 std::round() 函数（C++11起）或自定义逻辑来实现标准四舍五入。
对于更精确的控制，可以利用 std::nearbyint()、std::rint() 或 std::lround() 等函数，并结合银行家舍入规则。

C#:
Math.Round() 方法支持多种舍入模式，包括银行家舍入（通过 MidpointRounding.ToEven 参数）。

Ruby:
使用 round 方法，默认是半向上规则，但可以通过参数指定不同的舍入策略。

Go:
math.Round() 提供基础四舍五入，但需要自定义逻辑来实现特定的舍入规则。

PHP:
round() 函数允许指定模式，包括四舍五入到最接近的偶数，类似于银行家舍入。

案例：JS中tofix()并不是四舍五入

假如需求里说明数值保留1位小数，并四舍五入，
然后前端人员二话不说使用了toFixed()，那就掉坑了。
在W3C School中对tofix的描述是这样的：
https://www.w3school.com.cn/jsref/jsref_tofixed.asp

测试(1.45).toFixed(1)，结果为1.4

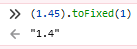
通过在火狐、Chrome、Edge、IE11上测试结果均为1.4，是foFixed函数的BUG吗？
也不算，因为ecmascript有详细规定toFix是如何计算的：https://262.ecma-international.org/6.0/#sec-number.prototype.tofixed
而各大浏览器的JS引擎遵循ecmascript去实现toFixed，则都会出现如上结果
如果我们业务中要求四舍五入，那么前端使用toFixed是不准确的，推荐方案是把浮点数转化为整数再计算

银行家算法示例

四舍六入五考虑，五后非零就进一，五后为零看奇偶，五前为偶应舍去，五前为奇要进一

import (
    "fmt"
)

func main() {
    fmt.Printf("9.8249    =>    %0.2f(四舍)\n", 9.8249)
    fmt.Printf("9.82671    =>    %0.2f(六入)\n", 9.82671)
    fmt.Printf("9.8351    =>    %0.2f(五后非零就进一)\n", 9.8351)
    fmt.Printf("9.82501    =>    %0.2f(五后非零就进一)\n", 9.82501)
    fmt.Printf("9.8250    =>    %0.2f(五后为零看奇偶，五前为偶应舍去)\n", 9.8250)
    fmt.Printf("9.8350    =>    %0.2f(五后为零看奇偶，五前为奇要进一)\n", 9.8350)
}

输出结果

  9.8249  =>  9.82(四舍)
  9.82671 =>  9.83(六入)
  9.8351  =>  9.84(五后非零就进一)
  9.82501 =>  9.83(五后非零就进一)
  9.8250  =>  9.82(五后为零看奇偶，五前为偶应舍去)
  9.8350  =>  9.84(五后为零看奇偶，五前为奇要进一)

为此，如果业务需要一定要四舍五入，测试人员要谨慎设计测试用例和数据。